I am very bad at math.
The next several hundred words will make that abundantly clear. But, despite me QEDing the internet a few weeks ago with irrefutable logic, I am now forced to revisit Ohio State's odds of college football glory based on nothing more than my utterly inadequate knowledge of things completely beyond the scope of my understanding.
No one asked me to do this, but in a sense, delving into a subject in which I have no background in (and indeed, have actively avoided for most of my life) makes me the most qualified person to tackle these important facts. I'm just a neutral outside observer, untainted by "expertise," so if you notice any glaring, obnoxious errors in either my math or logic perhaps it is you who needs to get off your high horse re-examine your understanding of the issue.
And the issue is football. And math.
Ohio State will (probably) play football this fall, starting in late October. I'm not sold that everything will go super smoothly from now until then, but let's assume that we all get to October 24th unscathed and undelayed. The Buckeyes will have nine games to get to playoff glory, and in all likelihood will have to kick a decent amount of ass to get there. That shouldn't be too much of a problem for Ohio State, especially with the return of Wyatt Davis and Shaun Wade, but going undefeated is still probably the baseline requirement for playoff entry in a shortened season.
So knowing that, I wanted to figure out two things: first, by how many points would Ohio State have to win every game to gain approval from the playoff committee? And secondly, how does the possibility of having to cancel games change that equation?
Turns out that the first question is pretty easy to answer. The Buckeyes famously beat the living hell out of the Wisconsin Badgers in the 2014 Big Ten Championship game by 59 points, propelling a team seen as a fringe playoff team to the fourth seed. As far as I can tell from seconds of exhaustive research, this is the baseline for the minimum amount of points needed by a marginal OSU team to gain entry into the playoffs.
So our job becomes pretty simple: just divide 59 by the number of games being played in the typical season. For instance, the Buckeyes played 13 games before the College Football Playoff in 2019, meaning that their wins had to come by a margin of at least, uh... hang on.

Yeah, that much. Here it is, expressed in fancy math equation form, where W(gs) is the Wisconsin game score, X(g) is the amount of games being played, and IWM is ideal winning margin.
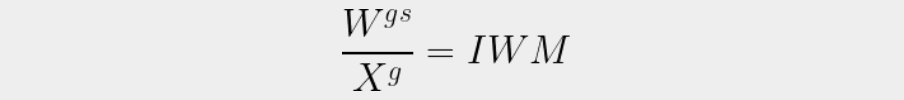
But we're only halfway there. Let's say that the unthinkable happens, and instead of things getting better and being great forever they somehow get worse and games end up canceled. "Hang on," you say, in a nasal whine, "you've already come up with a solution for this, remember? W(gs)/X(g)=IWM, I learned that in middle school!"
Ah, but therein lies the rub. The playoff committee isn't likely to cut the Buckeyes much slack for the Big Ten's extended football intransigence, so the more games they miss, the harder it'll be for them to get in. Logarithmically harder? No, that doesn't sound right. Maybe linearly more difficult? Exponentially? Wait, yes. That's it.
I'm not sure what "exponentially" means, but it looks right. And when I put it into a fancy internet calculator, I got this, which is wild. I didn't even know there was a "Brutus" setting on these things:

The easy way to interpret these results is to think of the y axis numbers as multiples of 59, the acknowledged total winning margin to gain entry to the playoff. So for instance, if Ohio State is forced to cancel one of their games, they'd have to win their remaining eight games by an average margin that's around 90% of 59, or 6.6ish points per game. If they cancel two games, they'd have to win their remaining seven games by an average margin that's around 2.6 times 59 divided by seven, or about 22 points per game. Cancel three games, and that margin jumps up to a very doable and coincidental 59 points per game.
Cancel four games, and things become a little more difficult for the Buckeyes, requiring them to win each game by 141 points. Cancel five games, and I'm not sure even Ohio State has the talent to get beyond the Big Ten Championship.
Granted, there are a lot of variables at play here, but luckily I've accounted for all of them in my unimpeachable equations.
Hopefully none of this comes to pass, but it's clear that the Buckeyes can afford to miss at least three Big Ten games and still be remembered forever as the team that won the 2020 national championship. Or alternatively, we could figure out a sound way to keep infections low, players safe, and get this thing done. But I guess that'd require a different kind of skillset than I have.


